Algoritma hashing disebut fungsi hash – mungkin istilah tersebut berasal dari gagasan bahwa nilai hash yang dihasilkan dapat dianggap sebagai versi “campur aduk” dari nilai yang diwakili.
Selain pengambilan data yang lebih cepat, hashing juga digunakan untuk mengenkripsi dan mendekripsi tanda tangan digital (digunakan untuk mengotentikasi pengirim dan penerima pesan). Tanda tangan digital diubah dengan fungsi hash dan kemudian nilai hash (dikenal sebagai message-digest) dan tanda tangan dikirim dalam transmisi terpisah ke penerima. Menggunakan fungsi hash yang sama dengan pengirim, penerima memperoleh intisari pesan (message-digest) dari tanda tangan dan membandingkannya dengan intisari pesan yang diterima juga. (Mereka harus sama.)
Fungsi hash digunakan untuk mengindeks nilai atau kunci asli dan kemudian digunakan nanti setiap kali data yang terkait dengan nilai atau kunci tersebut akan diambil. Jadi, hashing selalu merupakan operasi satu arah. Tidak perlu “reverse engineer” fungsi hash dengan menganalisis nilai hash.
Bahkan, fungsi hash yang ideal tidak dapat diturunkan dengan analisis tersebut. Fungsi hash yang baik juga seharusnya tidak menghasilkan nilai hash yang sama dari dua input yang berbeda. Jika ya, ini dikenal sebagai collision atau tabrakan. Fungsi hash yang menawarkan risiko tabrakan yang sangat rendah dianggap dapat diterima.
Berikut adalah beberapa fungsi hash yang relatif sederhana yang telah digunakan:
- Metode pembagian-sisa : Ukuran jumlah item dalam tabel diperkirakan. Angka itu kemudian digunakan sebagai pembagi ke dalam setiap nilai atau kunci asli untuk mengekstrak hasil bagi dan sisa. Sisanya adalah nilai hash. (Karena metode ini bertanggung jawab untuk menghasilkan sejumlah tabrakan, mekanisme pencarian apa pun harus dapat mengenali tabrakan dan menawarkan mekanisme pencarian alternatif.)
- Metode lipat : Metode ini membagi nilai asli (dalam kasus ini digit) menjadi beberapa bagian, menambahkan bagian-bagian bersama-sama, dan kemudian menggunakan empat digit terakhir (atau beberapa digit angka acak lainnya yang akan berfungsi) sebagai nilai hash atau kunci.
- Metode transformasi radix: Jika nilai atau kunci digital, basis angka (atau radix) dapat diubah menghasilkan urutan digit yang berbeda. (Misalnya, kunci angka desimal dapat diubah menjadi kunci angka heksadesimal.) Angka urutan tinggi dapat dibuang agar sesuai dengan nilai hash dari panjang seragam.
- Metode penataan ulang digit: Ini hanya mengambil bagian dari nilai asli atau kunci seperti digit di posisi 3 hingga 6, membalikkan urutannya, dan kemudian menggunakan urutan digit itu sebagai nilai atau kunci hash.
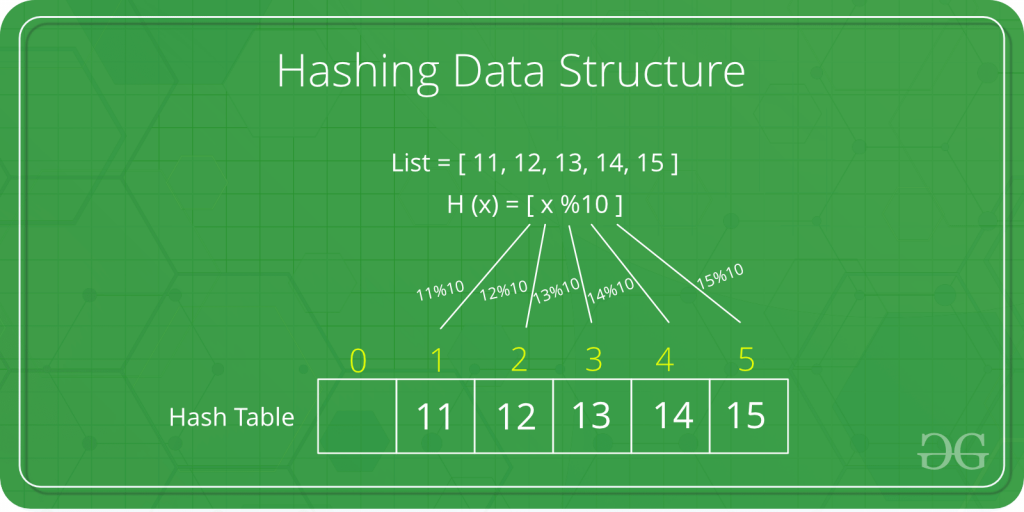
Hash Table adalah sebuah struktur data yang terdiri atas sebuah tabel dan fungsi yang bertujuan untuk memetakan nilai kunci yang unik untuk setiap record (baris) menjadi angka (hash) lokasi record tersebut dalam sebuah tabel.
Keunggulan dari struktur hash table ini adalah waktu aksesnya yang cukup cepat, jika record yang dicari langsung berada pada angka hash lokasi penyimpanannya. Akan tetapi pada kenyataannya sering sekali ditemukan hash table yang record-recordnya mempunyai angka hash yang sama (bertabrakan).
Pemetaan hash function yang digunakan bukanlah pemetaan satusatu, (antara dua record yang tidak sama dapat dibangkitkan angka hash yang sama) maka dapat terjadi bentrokan (collision) dalam penempatan suatu data record. Untuk mengatasi hal ini, maka perlu diterapkan kebijakan resolusi bentrokan (collision resolution policy) untuk menentukan lokasi record dalam tabel. Umumnya kebijakan resolusi bentrokan adalah dengan mencari lokasi tabel yang masih kosong pada lokasi setelah lokasi yang berbentrokan.
Operasi Pada Hash Tabel
- insert: diberikan sebuah key dan nilai, insert nilai dalam tabel
- find: diberikan sebuah key, temukan nilai yang berhubungan dengan key
- remove: diberikan sebuah key, temukan nilai yang berhubungan dengan key, kemudian hapus nilai tersebut
- getIterator: mengambalikan iterator,yang memeriksa nilai satu demi satu
Struktur dan Fungsi pada Hash Tabel.
Hash table menggunakan struktur data array asosiatif yang mengasosiasikan record dengan sebuah field kunci unik berupa bilangan (hash) yang merupakan representasi dari record tersebut. Misalnya, terdapat data berupa string yang hendak disimpan dalam sebuah hash table. String tersebut direpresentasikan dalam sebuah field kunci k.
Cara untuk mendapatkan field kunci ini sangatlah beragam, namun hasil akhirnya adalah sebuah bilangan hash yang digunakan untuk menentukan lokasi record. Bilangan hash ini dimasukan ke dalam hash function dan menghasilkan indeks lokasi record dalam tabel.
k(x) = fungsi pembangkit field kunci (1)
h(x) = hash function (2)
Contohnya, terdapat data berupa string “abc” dan “xyz” yang hendak disimpan dalam struktur hash table. Lokasi dari record pada tabel dapat dihitung dengan menggunakan h(k(“abc”)) dan h(k(“xyz”)).
Jika hasil dari hash function menunjuk ke lokasi memori yang sudah terisi oleh sebuah record maka dibutuhkan kebijakan resolusi bentrokan. Biasanya masalah ini diselesaikan dengan mencari lokasi record kosong
Deklarasi utama hash tabel adalah dengan struct, yaitu:
typedef struct hashtbl{
hash_size size;
struct hashnode_s **nodes;
hash_size (*hashfunc)(const char *);
}HASHTBL;
Anggota simpul pada hashtbl mempersiapkan penunjuk kepada unsur pertama yang terhubung dengan daftar. unsur ini direpresentasikan oleh struct hashnode:
struct hashnode_s {
char *key;
void *data;
struct hashnode_s *next;
};
Inisialisasi
Deklarasi untuk inisialisasi hash tabel seperti berikut:
HASHTBL *hashtbl_create(hash_size size, hash_size (*hashfunc)(const char *)){
HASHTBL *hashtbl;
if(!(hashtbl=malloc(sizeof(HASHTBL)))) return NULL;
free(hashtbl);
return NULL;
}
hashtbl->size=size;
if(hashfunc) hashtbl->hashfunc=hashfunc;
else hashtbl->hashfunc=def_hashfunc;
return hashtbl;
}
Cleanup
Hash Tabel dapat menggunakan fungsi linked lists untuk menghapus element
atau daftar anggota dari hash tabel .
Deklarasinya:
void hashtbl_destroy(HASHTBL *hashtbl){
hash_size n;
struct hashnode_s *node, *oldnode;
for(n=0; n<hashtbl->size; ++n) {
node=hashtbl->nodes[n];
while(node) {
free(node->key);
oldnode=node;
node=node->next;
free(oldnode);
}
}
free(hashtbl->nodes);
free(hashtbl);
}
Menambah Elemen Baru
Untuk menambah elemen baru maka harus menentukan ukuran pada hash tabel. Dengan deklarasi sebagai berikut:
int hashtbl_insert(HASHTBL *hashtbl, const char *key, void*data){
struct hashnode_s *node;
hash_size hash=hashtbl->hashfunc(key)%hashtbl->size;
Penambahan elemen baru dengan teknik pencarian menggunakan linked lists
untuk mengetahui ada tidaknya data dengan key yang sama yang
sebelumnya sudah dimasukkan, menggunakan deklarasi berikut:
node=hashtbl->nodes[hash];
while(node) {
if(!strcmp(node->key, key)) {
node->data=data;
return 0;
}
node=node->next;
}
Jika tidak menemukan key yang sama, maka pemasukan elemen baru pada
linked lists dengan deklarasi berikut:
if(!(node=malloc(sizeof(struct hashnode_s)))) return -1;
if(!(node->key=mystrdup(key))) {
free(node);
return -1;
}
node->data=data;
node->next=hashtbl->nodes[hash];
hashtbl->nodes[hash]=node;
return 0;
}
Menghapus sebuah elemen
Untuk menghapus sebuah elemen dari hash tabel yaitu dengan mencari nilai hash menggunakan deklarasi linked list dan menghapusnya jika nilai tersebut ditemukan. Deklarasinya sebagai berikut:
int hashtbl_remove(HASHTBL *hashtbl, const char *key){
struct hashnode_s *node, *prevnode=NULL;
hash_size hash=hashtbl->hashfunc(key)%hashtbl->size;
node=hashtbl->nodes[hash];
while(node) {
if(!strcmp(node->key, key)) {
free(node->key);
if(prevnode) prevnode->next=node->next;
else hashtbl->nodes[hash]=node->next;
free(node);
return 0;
}
prevnode=node;
node=node->next;
}
return -1;
}
Searching
Teknik pencarian pada hash tabel yaitu dengan mencari nilai hash yang sesuai menggunakan deklarasi sama seperti pada linked list. Jika data tidak
ditemukan maka menggunakan nilai balik NULL. Deklarasinya sebagai berikut:
void *hashtbl_get(HASHTBL *hashtbl, const char *key){
struct hashnode_s *node;
hash_size hash=hashtbl->hashfunc(key)%hashtbl->size;
node=hashtbl->nodes[hash];
while(node) {
if(!strcmp(node->key, key)) return node->data;
node=node->next;
}
return NULL;
}
Resizing
Jumlah elemen pada hash tabel tidak selalu diketahui ketika terjadi penambahan data. Jika jumlah elemen bertambah begitu besar maka itu akan mengurangi operasi pada hash tabel yang dapat menyebabkan terjadinya kegagalan memory. Fungsi Resizing hash tabel digunakan untuk mencegah terjadinya hal itu. Deklarasinya sebagai berikut:
int hashtbl_resize(HASHTBL *hashtbl, hash_size size){
HASHTBL newtbl;
hash_size n;
struct hashnode_s *node,*next;
newtbl.size=size;
newtbl.hashfunc=hashtbl->hashfunc;
if(!(newtbl.nodes=calloc(size, sizeof(struct hashnode_s*)))) return -1;
for(n=0; n<hashtbl->size; ++n) {
for(node=hashtbl->nodes[n]; node; node=next) {
next = node->next;
hashtbl_insert(&newtbl, node->key, node->data);
hashtbl_remove(hashtbl, node->key);
}
}
free(hashtbl->nodes);
hashtbl->size=newtbl.size;
hashtbl->nodes=newtbl.nodes;
return 0;
}
Lookup pada Hash table
Salah satu keunggulan struktur hash table dibandingkan dengan struktur tabel biasa adalah kecepatannya dalam mencari data. Terminologi lookup mengacu pada proses yang bertujuan untuk mencari sebuah record pada sebuah tabel, dalam hal ini adalah hash table.
Dengan menggunakan hash function, sebuah lokasi dari record yang dicari
bisa diperkirakan. Jika lokasi yang tersebut berisi record yang dicari, maka
pencarian berhasil. Inilah kasus terbaik dari pencarian pada hash table. Namun, jika record yang hendak dicari tidak ditemukan di lokasi yang diperkirakan, maka akan dicari lokasi berikutnya sesuai dengan kebijakan resolusi bentrokan. Pencarian akan berhenti jika record ditemukan, pencarian bertemu dengan tabel kosong, atau pencarian telah kembali ke lokasi semula.
Collision (Tabrakan)
Keterbatasan tabel hash menyebabkan ada dua angka yang jika dimasukkan ke dalam fungsi hash maka menghasilkan nilai yang sama. Hal ini disebut dengan collision.
contoh: Kita ingin memasukkan angka 6 dan 29.
Hash(6) = 6 % 23 = 6
Hash(29)= 29 % 23 = 6
Pertama-tama anggap tabel masih kosong. Pada saat angka 6 masuk akan ditempatkan pada posisi indeks 6, angka kedua 29 seharusnya ditempatkan di indeks 6 juga, namun karena indeks ke-6 sudah ditempati maka 29 tidak bisa ditempatkan di situ, di sinilah terjadi collision. Cara penanganannya bermacam-macam :
Collision Resolution Open Addressing
1. Linear Probing
Pada saat terjadi collision, maka akan mencari posisi yang kosong di bawah tempat terjadinya collision, jika masih penuh terus ke bawah, hingga ketemu tempat yang kosong. Jika tidak ada tempat yang kosong berarti HashTable sudah penuh.
2. Quadratic Probing
Penanganannya hampir sama dengan metode linear, hanya lompatannya tidak satu-satu, tetapi quadratic ( 12, 22, 32, 42, … )
3. Double Hashing
Pada saat terjadi collision, terdapat fungsi hash yang kedua untuk menentukan posisinya kembali.
Collision Resolution Chaining
1. Tambahkan key and entry di manapun dalam list (lebih mudah dari depan)
2. Kerugian:
- Overhead pada memory tinggi jika jumlah entry sedikit
3. Keunggulan dibandingkan open addressing:
- Proses insert dan remove lebih sederhana
- Ukuran Array bukan batasan (tetapi harus tetap meminimalisir collision: buat ukuran tabel sesuai dengan jumlah key dan entry yang diharapkan).
BINARY TREE
Binary Search Tree adalah sebuah konsep penyimpanan data, dimana data disimpan dalam bentuk tree yang setiap node dapat memiliki anak maksimal 2 node. Selain itu, terdapat juga aturan dimana anak kiri dari parent selalu memiliki nilai lebih kecil dari nilai parent dan anak kanan selalu memiliki nilai lebih besar dari parent. Pada artikel ini, penulis akan membahas bagaimana cara mengimplementasikan binary search tree di dalam Bahasa C.
Pertama, kita harus mempersiapkan struct yang melambangkan setiap node. Untuk contoh sederhana, struct yang dibuat disini hanya berisi 1 buah integer. Berikut adalah contoh structnya :

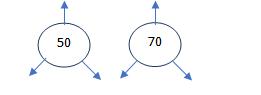
Setelah struct dibuat, kita akan membuat sebuah function yang digunakan untuk membuat node baru, seperti di bawah ini :
fungsi di atas berguna untuk membuat node baru. Jadi setiap createNode dipanggil, contoh createNode(50), createNode(70), maka akan jadi seperti ini :
setelah fungsi di atas sudah siap, berikutnya kita tinggal membuat fungsi insert/push menggunakan single pointer seperti di bawah ini :
Berikut adalah penjelasan dari code di atas :
- Pada if pertama, program akan melakukan cek pada root. Jika root bernilai NULL, artinya tree belum pernah terbentuk sama sekali. Karena itu kita tinggal melakukan malloc/ pemesanan memori pada root
- Pada else if kedua, program melakukan pengecekkan terhadap nilai baru yang mau diinsert. Jika nilai baru tersebut lebih kecil daripada node sekarang dan anak kiri dari node sekarang sedang kosong, maka program akan melakukan malloc pada anak kiri tersebut dan mengarahkan pointer parent kepada node yang sekarang.
- Pada else if ketiga, program akan melakukan pengecekkan seperti pada point 2. Hanya saja jika nilai baru tersebut lebih besar dari node sekarang dan anak kanan dari node sekarang sedang kosong, maka program akan melakukan malloc pada anak kanan tersebut dan mengarahkan pointer parent kepada node sekarang.
- Pada else if keempat, program akan jalan jika nilai baru lebih kecil dari node sekarang, tetapi anak kiri dari node tersebut tidak kosong. Maka program akan melakukan rekursif, memanggil fungsi push kembali dengan parameter nodel->left, yang berarti node sekarang dipindahkan ke anak kiri dan nilai a yang mau diinput. Sehingga pada tahap ini, suatu saat program akan menemui kondisi dimana anak kiri dari node sekarang sedang kosong.
- Pada else yang terakhir, program melakukan hal yang sama seperti point 4, hanya saja nilai yang dicek kondisinya harus lebih besar dari nilai node sekarang.
Jika kita ingin menggunakan double pointer, maka fungsi insert / push, akan jadi seperti ini :
Perbedaan cara memanggil fungsi single dan double pointer adalah seperti ini :
Contoh single : push(root,50);
Contoh double : push2(&root,50);
Jika dilihat dari code di atas, code double pointer terlihat lebih pendek karena dengan menggunakan double pointer, kita bisa melakukan passing by address. Sehingga ketika kita melakukan malloc atau memanggil newNode pada fungsi push2, maka root yang aslinya akan kena malloc juga. Berbeda dengan single pointer, jika kita melakukan node = newNode(a), maka root yang asli tidak akan ikut kena malloc, Karena ini merupakan passing by value.
~ Thankyou ~



No comments:
Post a Comment