Binary Search Tree

Binary Tree atau Pohon Biner adalah sebuah pohon dalam struktur data yang bersifat hirarkis (hubungan one to many). Tree salah satu bentuk struktur data yang menggambarkan hubungan hierarki antar elemen-elemennya (seperti relasi one to many). Sebuah node dalam tree biasanya bisa memiliki beberapa node lagi sebagai percabangan atas dirinya.. Secara khusus, anaknya dinamakan kiri dan kanan. Binary tree tidak memiliki lebih dari tiga level dari Root.
Binary tree adalah suatu tree dengan syarat bahawa tiap node (simpul) hanya boleh memiliki maksimal dua subtree dan kedua subtree tersebut harus terpisah. Tiap node dalam binary tree boleh memiliki paling banyak dua child (anak simpul), secara khusus anaknya  dinamakan kiri dan kanan.

Pohon biner dapat juga disimpan sebagai struktur data implisit dalam array, dan jika pohon tersebut merupakan sebuah pohon biner lengkap, metode ini tidak boros tempat. Dalam penyusunan yang rapat ini, jika sebuah simpul memiliki indeks i, anaknya dapat ditemukan pada indeks ke-2i+1 dan 2i+2, meskipun ayahnya (jika ada) ditemukan pada indeks lantai ((i-1)/2) (asumsikan akarnya memiliki indeks kosong).

Sebenarnya Binary Tree sama konsepnya dengan Tree. Hanya saja, kita akan mengambil sifat bilangan biner yang selalu bernilai 1 atau 0 (2 pilihan). Berarti, binary tree adalah tree yang hanya dapat mempunyai maksimal 2 percabangan saja. Untuk lebih jelasnya, lihat gambar di bawah ini.

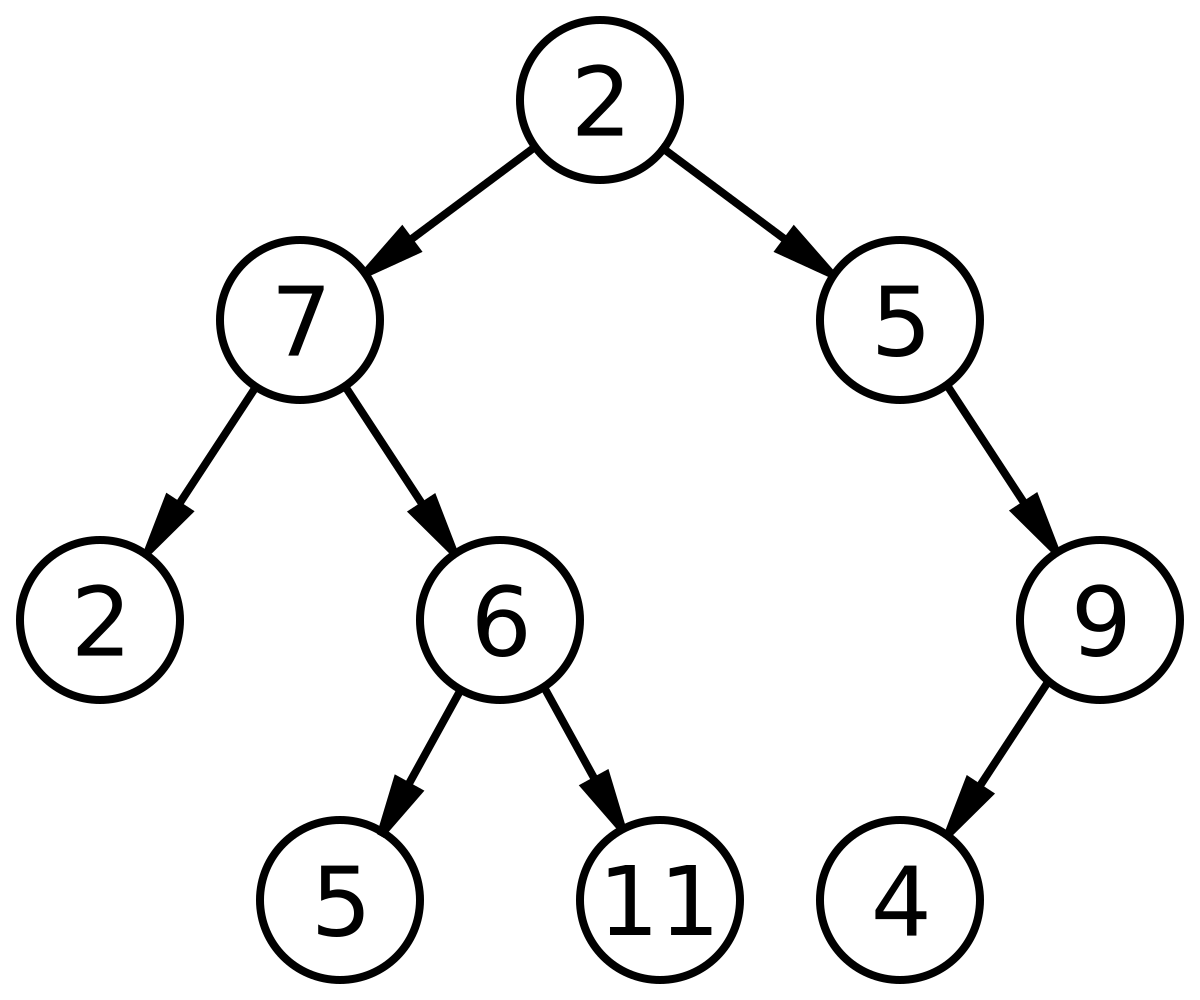
Binary Search Tree adalah tree yang terurut (ordered Binary Tree). Binary Search Tree juga sering disebut dengan Sorted Binary Tree yang berfungsi untuk menyimpan informasi nama atau bilangan yang disimpan di dalam memory. Dengan ini data dibagi menjadi dua dengan mencari titik tengah seagai patokannya. Binary tree terdiri dari simpul utama yang disebut dengan istilah root. Kemudian dari root tersebut terdapat bagian kiri dan bagian kanan. Data disimpan setelah root disimpan berdasarkan nilai perbandingan dengan root tersebut. Pengurutan dapat dilakukan bila BST ditelusuri (traversed) menggunakan metode in-order. Detail dari proses penelusuran ini akan dibahas pada pertemuan selanjutnya. Data yang telah tersusun dalam struktur data BST juga dapat dicari dengan mudah dan memiliki rata-rata kompleksitas sebesar O(log n), namun membutuhkan waktu sebesar O(n) pada kondisi terjelek dimana BST tidak berimbang dan membentuk seperti linked list.

Binary search tree memungkinkan pencarian dengan cepat, penambahan, juga menghapus data yang ada di dalamnya, bisa juga digunakan sebagai implementasi sejumlah data dinamis, atau pencarian table data dengan menggunakan informasi kunci atau key.
Agar data benar-benar tersusun dalam struktur data BST, dua aturan yang harus dipenuhi pada saat data diatur dalam BST adalah sebagai berikut:

- Semua data dibagian kiri sub-tree dari node t selalu lebih kecil dari data dalam node t itu sendiri.

- Semua data dibagian kanan sub-tree dari node t selalu lebih besar atausama dengan data dalam node t.

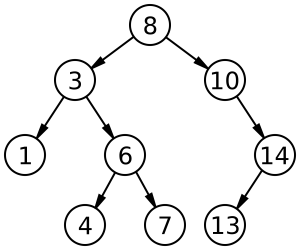
Pada dasarnya, operasi dalam binary search tree sama dengan operasi binary tree biasa, kecuali pada operasi insert, update, dan delete.

- Operasi insert, Pada binary search tree, insert dilakukan setelah ditemukan lokasi yang tepat (lokasi tidak ditemukan oleh user sendiri).

- Operasi search, Seperti pada binary tree biasa, namun disini update akan berpengaruh pada posisi node tersebut selanjutnya. Bila setelah diupdate mengakibatkan tree tersebut bukan binary search tree lagi, maka harus dilakukan perubahan pada tree dengan melakukan perubahan rotasi supaya tetap menjadi binary search tree.

- Operasi Delete, Seperti halnya update, delete dalam binary search tree juga turut mempengaruhi struktur dari tree tersebut. Pada operasi delete, diakukan terhadap node dengan 2 child, maka untuk menggantikannya, diambil node paling kiri dari right subtree

Lalu, ada 3 jenis cara untuk melakukan penelusuran data (traversal) pada Binary Search Tree:
- PreOrder : Print data, telusur ke kiri, telusur ke kanan
- InOrder : Telusur ke kiri, print data, telusur ke kanan
- Post Order : Telusur ke kiri, telusur ke kanan, print data

push

pre order

in order

post order

search

~ thankyou ~